Hej Numb3rsfans.
I dag snakkede Charlie om en del spændende matematik. Om det ligefrem spillede en rolle i opklaringen af forbrydelsen kan man nok tvivle på, men pyt med det. De opklarede jo sagen. Matematikken var bl.a. informationsteori, broerne i Königsberg, Steinerpunkter og sæbebobler. I må vente med Steinerpunkterne og sæbeboblerne til senere – måske i næste uge.
Informationsteori.
Charlie nævner informationsteori og siger noget om, at der er forskel på tilfældighed. Han snupper sin fars kryds og tværs og giver et eksempel: Hvis man skal finde næste bogstav i et ord, hvor man kender de første tre, er der nogle bogstaver, der er mere sandsynlige en andre.
Informationsteori er mange ting – flere sider i Encyklopædien – men Charlie mener nok matematisk informationsteori.
Ideen om, hvordan man kan give et mål for mængden af information i f.eks. en besked, der skal sendes over nettet, skyldes Claude Shannon i artiklen A mathematical theory of Communication fra 1948, hvor han bl.a. definerer informationsmængden, entropien. Entropi defineres via sandsynlighedsteori; man skal have et mål for, hvor meget klogere, man er blevet af at få en bestemt information. Vi forudsætter, at man på forhånd har en ide om, hvad der sandsynligvis kunne ske. Er beskeden så, at noget, vi anså for meget usandsynligt, er sket, vil vi anse det for mere information, end hvis vi får vished om, at noget, vi allerede mente var ret sandsynligt, rent faktisk er sket. Er informationen udfaldet af at slå et slag med tre terninger, vil jeg blive mere overrasket over 3 seksere, end over 2 seksere og en treer, fordi det sidste er et mere sandsynligt udfald (der er tre måder, man kan få 2 seksere og en treer svarende til, hvilken terning, der giver en treer). Man vil også blive mere overrasket over at få at vide, at det regnede i San Francisco i juni, end at det regnede i København. Så man måler informationen udfra, hvad man ved om sandsynligheden for de forskellige mulige informationer.
Et aspekt af informationsteori er at uddrage hvor lidt plads, der skal til for at repræsentere informationen – hvor mange bits. De bits, der er overflødige er redundante. Hvis vi ved, beskeden handler om et slag med en terning, behøver vi ikke bruge plads til at fortælle, at værdien er under 10, vi kan nøjes med et ciffer i titalssystemet og tre bits i totalssystemet. Inden vi skal sende beskeden vil vi forsøge at komprimere den mest muligt – smide overflødig information væk.
Et andet aspekt af sagen er, at man faktisk ofte sender overflødig information med: hvis man skal sende på en “kanal med støj”. Som f.eks. afspille en CD eller sende noget over nettet. Hvis beskeden risikerer at blive ændret lidt undervejs, vil man gerne kunne rekonstruere den. Det kan man f.eks., hvis man har sendt samme besked to gange, altså sendt overflødig information. Men det kan gøres noget mere intelligent – det er det, kodningsteori beskæftiger sig med. Se f.eks. Olav Geils hjemmeside. Hvor meget ekstra information, der skal med, afhænger af, hvor meget støj, der er på linien.
Broerne i Königsberg
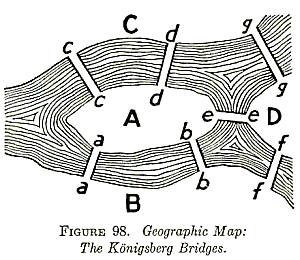
(fra Eric Weissteins Math World)
viser de syv broer i Königsberg (nu Kaliningrad). Königsbergbro problemet er: Findes der en gåtur, hvor man kommer over alle syv broer, kun en gang over hver, og starter og slutter samme sted.
Euler gav svaret: Nej, det gør der ikke. Og han gav et kriterie. Man kan betragte problemet mere generelt: Er der i grafen (igen fra Eric Weissteins Math World https://mathworld.wolfram.com)
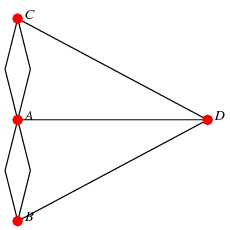
her en tur rundt, som starter og slutter i samme hjørne (en af de røde prikker) og passerer alle kanter præcis en gang. Svaret er for generelle grafer (punkter forbundet med kanter som ovenfor), at det er der, hvis og kun hvis der udfra alle hjørner går et lige antal kanter. Altså hvis hvert hjørne er forbundet til et lige antal andre hjørner. Se mere under Verdensår for Matematik.
Det er en væsentlig pointe, at det er fuldstændig ligegyldigt, hvilken facon landområderne har – derfor er de trukket sammen til de røde punkter. Den slags matematik hører til i algebraisk topologi, hvor vi studerer egenskaber ved geometriske objekter, som er mere kvalitative end afstand, areal, vinkel etc. Vi vil have lov til at strække vores objekter, men dog ikke rykke dem i stykker. Som når vi er ligeglade med, om vi ser på billedet af broerne eller figuren med røde punkter og kanter mellem dem. Man siger, at vi ikke kan se forskel på en kaffekop og en doughnut, men tro mig, DET kan vi. Matematikere er generelt ret glade for kaffe…
Mere om Steiner punkter og sæbebobler senere
Hilsen Lisbeth www.math.aau.dk/~fajstrup
numb3rs@math.aau.dk
