Bones of Contention. 2-10. Voronoi diagrammer og kulstof 14 datering.

Hej Bloglæsere.

Denne episode er bygget på bl.a. “The Kennewick Man”, som overhovedet ikke er matematik, men en blanding af arkæologi og politik. Se for eksempel her på about.com, eller National Park services Archeology Program
eller i Google. Åbenbart fandt man et skelet, der er ca. 10000 år gammelt, og det politiske går så på, om indianerne alligevel ikke er “de oprindelige” beboere i USA. Herunder, hvilken race skelettet havde, og hvem der har ret til at begrave det. Og hvad betyder det for rettigheder til land etc. En lang historie.

Matematikken var dels den matematik, der ligger bag kulstof 14 datering, (eksponentiel vækst) og dels Voronoi diagrammer. Jeg holder mig til Voronoi diagrammerne. Kulstof 14 kan man læse om på dansk mange steder på nettet; jeg er lige ved at tro, at Wikipedias danske version er ok på dette område. Lad mig nøjes med at gøre opmærksom på, at metoden blev indført i Danmark af Hilde Levi
Desuden havde antropologen data, som Charlie lagde ind i FORDISC, et program, der udfra en række data om kranier kan klassificere dem. F.eks. efter køn, men også efter om de hører til en af de 28 populationer, man har data om i “Howells databank”. Her er der jo noget statistik begravet, men jeg kender ikke programmet. Hvis man Googler FORDISC kan man se, at der (ikke overraskende) er en del debat om den slags klassifikation.

Voronoi diagrammer.

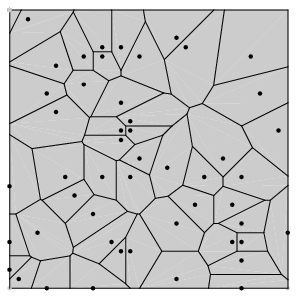
her er et Voronoi diagram (fra Eric Weissteins Mathworld https://mathworld.wolfram.com/VoronoiDiagram.html)
Man har på forhånd givet nogle punkter i (et stykke af) planen. Dette stykke af planen opdeles på en måde, så

• Der er præcis et af de oprindelige punkter i hvert område.
• Hvis man er i et af områderne, er det punkt, der ligger der, det punkt, der er tættest på – altså ligemeget hvor i det tilhørende område, jeg er.

En forklaring, jeg har snuppet fra min amerikanske blogkollega, er: Forestil jer en ørken med en masse vandautomater. vi vil lave en opdeling, så man altid ved, hvilken vandautomat, der er tættest på. Har man kun to punkter, er der en linie imellem, hvor man er lige tæt på begge punkter; de liniestykker, man ser i Voronoi diagrammmet er dele af sådanne midtnormaler. Er man på en af kanterne er man lige tæt på mindst to af punkterne. Man kan lege med det på denne applet fra Cornell – sæt punkter ind ved at klikke.
Man kan også lave rumlige Voronoi diagrammer – med samme specifikation. (Man kalder det også en Voronoitesselation).
På denne side, som er en del af en større samling af applets til geometri (også Steinertræer), lavet af Takashi Ohyami, kan man lave Voronoitesselationer udfra andre afstandsmål end det sædvanlige. Se også metriske rum fra tidligere på blogen.
Anvendelser er der masser af; og der er sågar en hjemmeside om Voronoi diagrammer, deres anvendelser etc.
Et eksempel er GIS-systemer. Vil man finde det nærmeste busstoppested, er det det stoppested, hvis Voronoiområde, man står i.

Min kollega, Jesper Møller, som har arbejdet meget med Voronoitesselationer i statistik, har fortalt mig om mange andre anvendelser:
Det bruges i biologi til at studere planter, der konkurrerer om plads, lys, etc. og til at modellere dyrs territorier.
Grævlinges territorier modelleres for eksempel som Voronoidiagrammer med grævlingehuler som udgangspunkt.
I økonomi kan man vurdere, hvor mange forbrugere, der vil bo tættest på et nyt supermarked med forskellige mulige placeringer, før man rent faktisk placerer det nye supermarked. (Charlie forklarede det med burgerrestauranter). Bygger man IKEA i Aalborg, har man uden tvivl overvejet, hvor mange kunder, der vil foretrække at tage dertil og ikke til IKEA i Århus. (Det er nok ikke kun et spørgsmål om afstand, eller i hvert fald er det afstand målt i tid og ikke fugleflugtslinie).

Galakser ser ud til at være koncentreret om sideflader, kanter og især hjørner af en 3D Voronoi-tesselation af rummet. Og hvad er så “punkterne”, altså kernerne i Voronoi-tesselationen? Jeg har, via Jesper, fået en forklaring fra astrofysikeren Rien van de Weygaert, og når man ikke er vant til at færdes blandt astrofysikere, kan man godt blive lidt svimmel af den slags:
Voronoimodellen (kosmisk “skum”) forklares ved, at man i Universets tidlige fase havde en meget jævn (uniform) fordeling af masse, men dog med lidt variation, så der var steder med midre massetæthed og steder med højere tæthed. Som tiden går, vil masse tiltrækkes til de områder, hvor der er højere tæthed, og det er selvforstærkende, så man får mere og mere masse nogen steder, og tomrum de steder, hvor der i starten var lavere massetæthed. Der er mange kræfter, der virker: tyngdekraft, hydrodynamik, dannelse af stjerner, supernova eksplosioner etc. og astrofysikerne har ikke styr på hele det samspil.
Men den information, vi har, tyder på, at galakserne danner en slags “skum” struktur – ligesom sæbeskum.
Galakserne sidder, hvor tætheden oprindeligt var størst, og imellem er der tomrum, som oprindeligt var minima i tætheden af masse.
Rien skriver meget poetisk, at det er “et ocean af mørkt stof og galakserne sidder på toppen af de højeste tårne (mest tæthed) af mørkt stof”. At det er en Voronoitesselation, der bedst beskriver skummet, skyldes bl.a., at de kan varieres og komme til at passe med mange forskellige antagelser om universet, og når man skal bruge statistiske metoder til at se, hvilken struktur, der passer bedst til data, er det godt at have en fleksibel struktur.
Det samme gælder anvendelserne i biologi etc., hvor man også skal have strukturen til at passe med noget kendt data.

Charlie ville modellere placering af bosættelser udfra kendskab til naturlige ressourcer som floder; på den måde ville han finde gravpladser. Man modellerer faktisk bosættelser på den måde, men det kunne nu ikke bruges til noget i serien…

Hilsen Lisbeth www.math.aau.dk/~fajstrup
numb3rs@math.aau.dk