Der var temmelig heftig matematik med denne gang:
Ito Stratonovich driftintegraler (Analyse af flystyrtet)
Heterogen Poisson proces (Charlies analyse af indbruddet)
Wavelet baseret dekonvolutionsalgoritme (slørede fingeraftryk rekonstrueret)
Strange Loop theory (ledte tilbage til det skumle programs forfatter)
Wavelet baseret dekonvolutionsalgoritme
Sådan en har vi set tidligere i Numb3rs. Man har et billede, der er tværet lidt ud – f.eks. ved, at man har det i en lav opløsning – få pixels, eller ved, som i dette Numb3rs afsnit, at nogen har gnedet et fingeraftryk lidt ud. Kan man få flere pixels med, altså rekonstruere det rigtige billede?
Det kan man faktisk gøre forbavsende effektivt. Ideen er som følger: Det udtværede billede er fremkommet ved, at man tager en slags middelværdi – et grovkornet billede har en større ensfarvet grå firkant i stedet for de 4 underliggende mørkegrå og lysegrå.
Der er altså en sammenhæng mellem det fine billede og det grove ved at “midle”. Så man skal “midle tilbage igen”.
Det kan man ikke umiddelbart gøre. Det er et “ill posed” problem. Der er flere muligheder for, hvordan billedet kunne have set ud, inden midlingen. Men der findes metoder til “udfoldning, dekonvolution”. En af dem involverer at beskrive billedet ved brug af wavelets, som Kenneth har beskrevet under “Provenance”, og Arne Jensen har skrevet om det til bloggen her. Det grovere billede betragtes som en wavelet beskrivelse, hvor der mangler noget af den finere information – og pointen er, at hierarkiet i wavelets ikke er som i beskrivelsen med en pixel ad gangen, hvor en underdeling i flere pixels blot giver flere ensfarvede pixels til erstatning for en pixel. Wavelets er en bedre tilgang til at “midle tilbage igen”.
I det sidste link finder man et 32×32 pixel billede af Lincoln, som ved hjælp af wavelets forfines til et 128×128. Det er uhyre overbevisende!
“Ito Stratonovich drift integrals”
Ito og stratonovich er to matematikere, og der refereres til to forskellige tilgange til integraler, vel at mærke af stokastiske differentialligninger. Det er overordentlig langhåret matematik, som bl.a. bruges i matematiske finansiering. Når man har en ide om, hvordan noget udvikler sig, og denne beskrivelse involverer noget “støj” – som man kan beskrive ved sandsynligheder. Det er den slags beregninger, der åbenbart indgår i at beskrive, hvordan vragdelene spredes efter et flystyrt.
Der findes også forskellige integraler af funktioner uden stokastiske bidrag.
I gymnasiet møder man mest integralet som areal under en graf. Eller som en stamfunktion evalueret i endepunkterne. Det er Riemann integralet, der ligger til grund for den tilgang. Men der findes andre integraler, som kan håndtere en større klasse af funktioner. Lebesgue integralet er den bedst kendte generalisering.
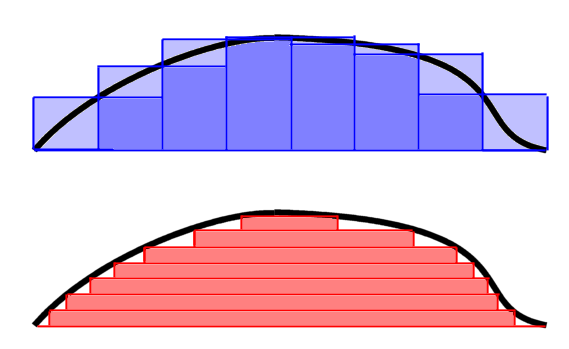
Man kan tænke på Riemann integralet som en approksimation til arealet under kurven med smallere og smallere rektangler på højkant, i.e., man inddeler mere og mere langs x-aksen. Lebesgue integralet er “på den anden led” – rektangler på langs, så inddelingen langs y-aksen forfines mere og mere.
På billedet man se hvordan – det er Riemann for oven og Lebesgue for neden. I Riemann integralet forlanger man, at det samlede areal af de kasser, der “stikker ovenfor”, nærmer sig det samlede areal af de kasser, der stikker nedenfor, når inddelingen bliver fin nok. Hvis funktionen hopper i et punkt – så f(x)= 2x bortset fra f(2), som er 17 – bliver det tilsvarende areal i begge tilfælde det samme, som hvis den ikke hoppede. Men en funktion, der hopper rigtig tit, som funtionen, der er 1 for alle rationale tal og 0 ellers, er ikke Riemann integrabel. Den er Lebesgue integrabel og integralet giver 0.
Strange Loops
Mærkelige løkker… Her bliver jeg helt nostalgisk. For mange år siden, da blogskribenten var noget yngre, udkom bogen “Gödel Escher Bach, an eternal golden braid.” af Douglas Hofstadter. Den blev en slags kult. Og man burde læse den. Jeg købte den, men kom med skam at melde aldrig igennem den. Det er derfra, ideen om strange loops stammer. Et strange loop er en bevægelse “opad” og “rundt”, hvor man ender, hvor man startede. Som i den Escher tegning, Charlie viste. Andre eksempler findes i musik, hvor man f.eks. hos Bach kan modulere opad i toneskalaen, men alligevel ende tilbage, fordi man ender ved sammen grundtone. Man kan høre et eksempel her på wikipedia
Hofstadter har mange referencer – det er en lang bog, og jeg har den stadig – i matematik er strange loops bl.a. den slags paradokser, der opstår ved selvreferencer:
Manden, der siger “jeg lyver”.
Grellings paradoks: Kald et ord heteorologisk, hvis det ikke beskriver sig selv. Er ordet “heteorologisk” så heteorologisk?
Russels paradoks: Lad M være mængden af mængder, der ikke tilhører sig selv. Er M da et element i M?
Eller Halfdan Rasmussens løsning af barber-paradokset (Barberen barberer alle dem, der ikke barberer sig selv. Hvem barberer så barberen?)
Øen i søen har kun en barber
Til gengæld så klipper han alt hvad han ser.
Han klipper sin fætter, sin hund og sit får
Han klipper billetter, når færgerne går
Han klipper sin plæne, sin hæk og sit hegn
Men selv er han skaldet som Roskildevej’n
Charlie påstår, at man kan finde en ophavsmand til et virusagtigt program ved at følge et strange loop. Det ved jeg ikke, om han har ret i, men dataloger er velkomne til at bidrage! I dette tilfælde skulle programmet jo aktiveres udefra, så måske opstår der en slags loops i den forbindelse.
Der er masser af referencer til strange loops på nettet. Det er vist stadig kult. Imponerende, når man tænker på, bogen er fra 1979.