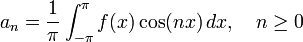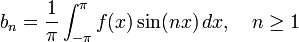Numb3rs

Matematikken blev ikke holdt frem i lyset, som den plejer – men den var der jo alligevel: Robotten/computeren, der forstod almindelig tale; søgning i store datamængder, ekspertsystemer – altsammen noget, der har krævet masser af matematik. Men jeg vover også at skrive om noget andet, som var meget centralt, nemlig Turing test. Titlen, First Law, henviser til Isaac Asimovs regler for robotter: Asimov Online.
Første lov er: Robotter må ikke slå mennesker ihjel. (Ikke skade mennesker eller lade stå til, mens mennesker bliver skadet.)
Anden lov. Robotter skal adlyde mennesker med mindre dette overtræder første lov.
Tredje lov: En robot må beskytte sig selv, så længe dette ikke er i modstrid med de to første love.
Man kan således konkludere, at robotter brugt i krig ikke er robotter…
Ekspertsystemer
Der er mange former for ekspertsystemer. De bruges som beslutningsstøttesystemer til eksempelvis revisorer eller læger. Et dansk firma, som jeg rigtig gerne henviser til, er Hugin. Man kan hente en demoversion af Hugin, som man kan lege med, hvis man ikke har et alt for stort netværk. Hugin er grundlagt af bl.a. Steffen Lauritzen, min gamle kollega, som nu er professor i Oxford og Finn Verner Jensen, som er professor i datalogi. (Om bayesianske netværk er datalogi eller matematik, er der ikke noget fornuftigt svar på. Steffen og David Spiegelhalter publicerede i 1988 en uhyre effektiv algoritme til “opdatering” (belief propagation) i Bayesianske netværk, som er hjertet i beslutningsstøttesystemer. Man kan læse en fin introduktion til Bayesianske netværk i denne artikel i Naturens verden.
Et Bayesiansk netværk beskriver mulige årsagssammenhænge. E.g. Hvis man har lungebetændelse, er der en vis sandsynlighed for, at man hoster. Hvis man ryger, er der en vis sandsynlighed for, man hoster. Hvis man har bronkitis er der en vis sandsynlighed for, man hoster, har man influenza hoster man måske etc. Så, hvad gør en læge, når en patient fortæller, at hun hoster? Hvad er den mest sandsynlige diagnose?
Hvis nu det er influenzasæson, så er den mulighed mere oplagt.
Der er altså endnu en sammenhæng; hvis det er influenzasæson er der en vis sandsynlighed for, at patienten har influenza.
Har patienten feber, spiller det tilbage: Har man influenza har man med en vis sandsynlighed feber, har man lungebetændelse kan man også have feber. Bayes’ formel kan vende sandsynligheder om: Fra symptomerne tilbage til de mulige årsager fra feber tilbage til sygdomme, fra feber OG hoste tilbage, fra feber OG hoste OG influenzasæson tilbage. Jo mere, man ved, jo bedre diagnose.

Nedenfor  er et eksempel på et Bayesiansk netværk. Dyspnoea er kortåndethed. I knuderne (boblerne) står sandsynligheden for eksempelvis at en tilfældig person har kræft.

Der er for alle pilene tilkyttet sandsynligheder: HVIS man har tuberkulose eller kræft, (samlet i TbOrCa), så er der en vis sandsynlighed for at være kortåndet. Har man ikke tuberkulose eller kræft er sandsynligheden mindre (men nok ikke 0). HVIS man har været i Asien er sandsynligheden for at have tuberkulose større, end hvis man ikke har det.

Man indtaster nu f.eks., at patienten er kortåndet og har været i Asien. Softwaren opdaterer nu sandsynlighederne i de forskellige “knuder ” (belief propagation) . I knuden om kræft står nu sandsynligheden for at have kræft forudsat, man er kortåndet OG har været i Asien. Måske indtaster jeg, at patienten ikke ryger. Igen opdateres (sandsynligheden for cancer falder så i forhold til den, der står der nu ). Opdateringen er i princippet simple regneoperationer med brug af Bayes’ formel, men der er rigtig mange af dem og Lauritzen Spiegelhalter algoritmen organiserer disse regninger rigtig smart.

Samme typer underliggende net bruges, når ekspertsystemer lærer. 

Turing test
Alan Turing var ansat i Bletchley Park, briternes dekrypteringssted, hvor omkring 10000 mennesker arbejdede med brydning af tyskernes krypterede beskeder, herunder Enigma. Turings ideer er grundlag for meget moderne datalogi. Især den del, der handler om, hvad man overhovedet kan få en computer til. Turing gav en abstrakt beskrivelse af en maksine, der udfører en algoritme – en Turing maskine. Det har Hans Hüttel fortalt om tidligere på bloggen
Turing test er noget helt andet, som også skyldes Alan Turing: Hvordan kan man afgøre, om man taler (eller skriver) med en robot eller med et menneske.
Turing testen er følgende test. Et menneske C skal ved at konversere (skrive replikker til og modtage replikker fra) A og B, hvoraf en er en computer, den anden et menneske. Kan C ikke kende forskel, har computeren bestået Turingtesten.
Spørgmålet om, om man kan lave maskiner, der kan tænke – kunstig intelligens – har været emne både for filosoffer og matematikere som Turing. Om det er det, man tester, i en Turing test, er omdiskuteret. Ligesom i Numb3rs her, har man lavet programmer, chatbots, som er designet til netop at bestå Turingtesten. Og så kan de ellers ikke meget andet. (Et eksempel er ELIZA, som er meget simpelt, men ret morsomt alligevel.) Pointen er, at de svarer tilpas vagt, og dermed giver indtryk af at forstå. Lidt ligesom col readings blandt clairvoyante.
Nogle danske chatbots Knud fra Odense Kommune, Emma fra forbruger Europa og Betty fra Frederiksberg Kommune. Disse bots er kun gode til det, de skal på de sites, de hører til. Så de skal kun svare fornuftigt på et begrænset antal spørgsmål. Hvis botten fra kommunen genkender ordet “pas”, kan den linke til den rigtige side. Eller spørge, hvad man mere præcist vil.
En omvendt Turing test
Kan man omvendt få en computer til at skelne mellem andre computere og mennesker? Det gør man med Captcha. Completely Automated Public Turing Test To Tell Computers and Humans Apart. De forvredne tekster, man skal læse og taste ind, for at få lov at skrive kommentarer visse steder. De er opfundet af L. von Ahn, M. Blum, N.Hopper og J.Langford fra Carnegie Mellon.
Men det er altså ikke en Turing test. Se i øvrigt også GWAP, hvor man efter sigende kan lære computere at blive bedre til noget, mennesker normalt er bedst til. Hvis altså, man selv er bedre 🙂

Matematikken var økonomisk modellering. Og noget med matematikken i basketball. Det er rigtigt, at CalTech, som jo er modellen for CalSci i serien, taber stort i sport. De optager studerende efter deres akademiske kvalifikationer, og så er det nok ikke let at slå andre universiteter med sportsstipendier.

Økonomiske modeller
Der er faktisk folk, der laver økonomiske modeller for narkomarkedet; f.eks. A search theoretic model of the retail market for illicit drugs. og Optimal law enforcement and the economics of the drug market: Some comments on the Schengen Agreements af Nuno Garoupa. Så det er ikke helt urealistisk, at man faktisk bruger den slags. Omend det nok ikke er helt så simpelt som det ser ud her.
I Illicit Drug Markets and Economic Irregularities ser man på, hvordan narkomarkedet afviger fra sædvanlige økonomiske modeller. Og det er jo det, Charlie finder ud af.

I får lidt om sædvanlige økonomiske modeller. Skal I se på narkohandel, må I kigge på artiklerne ovenfor.

Lad os se på en enkelt vare. Udbud afhænger af prisen (kan jeg få mange penge for at producere grise, vil jeg gerne producere mange), Efterspørgslen afhænger også af prisen, men det er omvendt. Er prisen høj, vil jeg ikke købe så meget svinekød.

I en slags auktionsmodel udbydes en vis mængde, S. (for Supply)

Hviv nu efterspørgslens afhængighed af prisen er D=ap+b hvor p er prisen, mens a og b er nogle konstanter (a er negativ – højere pris giver mindre efterspørgsel).

Så vil den udbudte mængde S blive solgt til prisen p=(S-b)/a hvis vi siger, alt skal sælges S=D.

Lad S=cp+d. Så vil man i en ligevægt mellem udbud og efterspørgsel have S=D, altså ap+b=cp+d (skæring mellem to linjer) og vi får p=(b-d)/(c-a). Men hvordan opstr sdan enligevægt, om overhovedet. Lad os sige, vi udbyder nogle grise nu – S1 ialt- og får prisen p1 for dem (p1=(S1-b)/a). Så træffer vi beslutning om at udbyde S2=c(p1)+d næste gang (til tiden t2)- det tager tid at fodre dem op. Til tiden t2 bliver de solgt til prisen p2=(S2-b)/a og så videre. Og hvad sker der så? Nedenfor er en illustration af netop dette. Bemærk, at prisen er opad y-aksen, så man skal enten vende det om i hovedet eller skrive udtrykkene om til pD=(D-b)/a og pS=(S-d)/c. Bemærk, hvordan udviklingen er ind mod ligevægtspunktet.

 Figuren er fra Wikipedia Commons.http://en.wikipedia.org/wiki/Cobweb_model

Prøv at eksperimentere med hældningerne af de to linjer. Det er ikke altid, udviklingen går ind mod ligevægtspunktet…

Modellen kaldes ofte grisecyklen 🙂 The hog cycle, fra artiklen Die Prognose der Schweinepreise fra 1928.
Man kan naturligvis variere en sådan model – S og D er nok ikke lineære funktioner af p. – Man kan måske lagre varerne (ikke grise, men andre varer) . – Måske tror producenterne ikke, at prisen i næste periode er den samme – forventet pris – så udbud til tiden t+1 afhænger af prisen til tiden t på en mere indviklet måde. man kan lege med økonomiske modeller på http://www.econmodel.com/classic/cobweb.htm

Der er masser af matematiske modeller i økonomi. Vil man være rigtig god til den slags, kan man passende læse matematik-økonomi (mat-øk) i Aalborg, Århus, Odense eller København (Og ja, det var en reklame…).

Charlie blev brugt en hel del. Han lavede en model af beslutninger i et nævningeting. Analyserede software fra databasen med lægdommere (domsmænd og nævninge i DK – jury i USA). Der var pseudotilfældige tal, frembragt ved Mersene twostor metoden. Og så var der noget om gruppedynamik, som vel også kan modelleres matematisk – mere eller mindre effektivt 🙂

Jeg er sent på den med dette indlæg, så I må nøjes med

Pseudotilfældige tal

Tilfældighed kan kvantificeres. Det er det, man gør i sandsynlighedsteori og statistik. Man kan have uniformitet, hvor alle de mulige udfald har lige stor sandsynlighed, eller man kan have en underliggende struktur, der gør, at noget er mere sandsynligt end andet. I lotto vil man f.eks. gerne have, alle kombinationer er lige sandsynlige. Det samme, når man slår med en terning.
Pseudotilfældige tal er (følger af) tal, der i virkeligheden er fuldstændig forudsigelige, men som udefra ser helt tilfældige ud (uniformt fordelt). Man har brug for at generere tilfældige tal mange steder. I dette afsnit var det (så vidt jeg husker) tilfældig udvælgelse af domsmænd, det drejede sig om.
Vil man have rigtig tilfældighed kan man f.eks. bruge kvantefysik – et stof, der henfalder. Men det er besværligt. Pseudotilfældighed kan ofte være nok, og Charlie omtaler en frembringer af tilfældige tal, en PRNG (Pseudo Random Number Generator), Mersenne twister fra artiklen Matsumoto og Nishimura
Mersenne Twister: A 623 dimensionally equidistributed uniform pseudorandom number generator fra 1998.

En frembringer af pseudotilfældige tal skal bruge nogle inputværdier og leverer så en stribe tal, som er fuldstændig bestemt at disse inputværdier. (Mersenne twister bruger Mersenne primtal, som er primtal på formen 2^p -1 . Det er et uløst matematisk problem, om der findes uendelig mange primtal på den form. Men vi kender 47 ialt :-)) Den talfølge, der frembringes af Mersenne twister gentager først sig selv efter mere end 10^(6000) tal.  Talfølgen er tal med 32 bits i hvert (32 cifre i 2-talssystemet). Der er forskellige mål for, hvor tæt en PNRG er på at ligne det, man ville få ved at trække hvert tal tilfældigt (uniformt). Det vil jeg se, om jeg kan få en statistiker til at skrive noget om. Mersenne twister er god, fordi den er hurtig. (Se mere på Wikipedia om, hvordan den præcis virker).

En anden og mere sikker PNRG er Blum Blum Shub. Den er langsom, men det er ikke altid, det skal gå hurtigt – måske er sikkerhed vigtigere.
Man finder to primtal, p og q, som er meget store. Så ganger man dem og får M=pq. Nu vælges en startværdi. Talfølgen er givet ved at tage det seneste tal i rækken, xn, kvadrere det og udregne resten ved division med M.
Eksempel: p=7, q=11, så er M=77. Lad x0=15, så er x0^2= 225. Divider med 77. Resten er 225-154= 71.
Næste tal 5041-5005=36, 1296-1232=74, 5476-5467=9, 81-77=4, 16, 256-231=25
15, 71, 36,74,9,4,16,25
det ser da ret tilfældigt ud. Man bruger ikke direkte tallene fra output, men genererer en bit fra hvert af disse tal – f.eks. et 1 tal, hvis der er et ulige antal 1’er i xn skrevet binært…

Et afsnit om mænd, der samler på sko – altså sneakers. Matematikken var bl.a. brydning af en “stemmekontrol” ved brug af wavelets. Noget om skibbrud og gummisko. Hyperspektral billedanalyse. Og så fik Charlie lavet et par sneakers med matematiske symboler på – andre matematikere køber Georg Jensen Møbius smykker, og sådan er vi så forskellige.
Hyperspektral billedanalyse
Det var den teknik, Charlie og Larry brugte til at analysere sneakers, uden at behøve at skære dem i stykker. Jeg skrev om det under Charlie don’t surf, og det er, så vidt jeg kan se, ikke helt det samme her, men næsten. Kort sagt drejer det sig om at analysere indmaden af skoen udfra kendskab til elektromagnetisk refleksion eller absorption (tror jeg nok) med mange frekvenser. Ordet Hyper skyldes, at man tager frekvenser fra det ikke synlige spektrum med. I den tidligere episode drejede det sig om flybilleder af et område. Her så det ud til, at de fik information om spektret fra et lille 3D område (et antal voxels og i stedet for de 2D pixels). Man kender så den samlede reflektion fra et større område – mange frekvenser og vil gerne for eksempel udlede, hvilket (hvilke) materiale(r), der kan udsende dette spektrum.
Her er et billede fra NASA (ikke gummisko, men teknikken er den samme)

Her er det 2D billeder – de forskellige frekvenser er det, der er afbilledet i den tredje dimension. Nasa bruger teknikken i satellitter. Se mere på Remote sensing tutorial introduction. Den slags teknik er fyldt med matematik. Her er f.eks. en artikel fra University of Minnesota:Spatially Coherent Non-linear dimensionality reduction and segmentationof hyper spectral images af Mohan, Shapiro og Bosch.
De ser på problemet med at komme fra den store mængde data, der ligger i spektrene, til et 2D billede. Et (blandt mange) af de gode problemer er, hvordan man finder værdien af hver enkelt pixel (værdi=farve) og holder styr på, at det giver mening, når man ser på nabo pixels og desuden husker, at det skal komme fra noget virkeligt.
Hvert punkt har 3 rumlige koordinater og desuden værdier fra de spektre, man har optaget. Dette repræsenteres som et højere dimensionalt objekt; hvis man kender 200 spektre, er det hele 3+200 dimensionalt. Tænk på hvert punkt repræsenteret med en stribe koordinater (x,y,z, f1,f2,f3,…,f200), hvor f’erne er spektrenes værdi i det punkt og x,y,z er rumlige koordinater. Men det er lidt mere indviklet – hvis man vil være rigtig svimmel, kan man tænke på, at dette 203-dimensionale objekt ligger inde i et måske 500 dimensionalt rum, ligesom en 2-dimensional overflade kan ligge i et 3D rum.
Pointen er, at den 2D repræsentation, man laver – (med farver, så det er faktisk højere dimensionalt) – skal repræsentere dette 203D objekt. Og det er ikke simpelt. Desuden er der statistik i at sortere støj fra. Noget data er “skævt” eller helt i skoven.
Skibbrud og gummisko
Det er rigtigt, som Amita og Charlie siger, at man analyserer havstrømme ved at se på, hvor vraggods fra skibbrud ender. Det eksempel, de tænker på, er 33000 Nike sko (og 17000 dåser med nudler…) fra et skibbrud ud for Californien. Men hvordan det kan bruges i opklaringen her, forstod jeg ikke.
Stemmelås
De bryder ind i skoskabet ved at afspille den rigtige sætning med den “rigtige” stemme, eller rettere: de imiterer den rigtige stemme ved at sammensætte bidder af andre stemmer. Pointen her er, at sproglyde kan sammensættes af mindre bidder – phonemer. Der er åbenbart 44 phonemer på engelsk. Det kommer selvfølgelig an på, hvor fint man skelner. Ideen er, at man som udgangspunkt har uendelig mange muligheder, hvis man vil afspille “Matematik er fantastisk nyttigt”, som jeg ville sige det. Men hvis man deler sætningen op i phonemer, er der kun tilbage at finde ud af, hvordan jeg udtaler hvert af disse. Der kan man bruge en database med mange forskellig lydoptagelser med andre mennesker og stykke dem sammen, til man rammer min måde at tale på.

Jeg bemærkede “Forensic Audiology”, Støj filtre, Levy flight path, multilayer encryption. Og desuden noget om, at der var for mange 8-taller på Mah Jong siden med piger til salg. Og for mange 9-taller på den, hvor de skulle sælges som “spøgelsesbrude”.

Signalbehandling, Forensic audiology
Et lydsignal kan være en blanding af mange forskellige lyde. Kender man en af disse lyde, kan man “trække den fra” signalet og få fokus på de andre lyde. Man kan analysere signalet for at finde ud af, hvor det er optaget ved at lede efter lyde fra tog, fly, kraftværker etc. Det er meget smart og meget vanskeligt.
Signalet fra en mobiltelefon (det var det, der skulle analyseres her) er digitalt – man har omsat lyd til tal. Så det drejer sig om digital signalbehandling, DSP (Digital Signal Processing). Amita talte om frekvensområde analyse og forskellige filtre. Matematikken bag signalbehandling er bl.a. Fourier-, Laplace-, wavelets og Z-transformation. Hentydningen til frekvensområde analyse må være til Diskret Fourier transform, så vidt jeg kan se, men til sagen – et lille hjørne af sagen i hvert fald.

Et lydsignal kan se meget indviklet ud. Her er et ikke særlig indviklet eksempel:

Tiden er langs den vandrette akse og lodret afbildes sammenpresning eller udvidelse af luften – en lydbølge er en trykbølge.
På billedet er den røde kurve summen af de to andre, lad os kalde den g(t). Den grønne er grafen for sin(t) og den blå er 1/2 sin(3t). (Jeg har brugt dette eksempel i Guns and Roses). Så i stedet for at fortælle, hvad g(t) er, kunne jeg skrive tallene 1, 1 (for 1 gange sin(1t) ) og 1/2,3 for (1/2 sin(3t)) Hvis vi altså er enige om, at vi vil skrive funktionen som en sum af en masse funktioner a sin(bt) og vil oplyse hvilken sum ved at give listen af a’er og b’er. Det sprer jo meget plads.
Hvis man vil skrive en lyd f(x) som sum af sinuskurver og cosinuskurver,

 

(en uendelig sum  -skal læses a1 cos(1x)+b1sin(1x)+a2 cos(2x)+b2 sin(2x) +…) så gælder det om at finde koefficienterne a1,…. og b1,…. og det kan man ved integration:

og

Det giver ikke altid mening – man kan ikke altid udregne integralerne og den uendelige sum giver ikke altid noget meningsfyldt, og selv hvis den gør, giver den ikke altid f(x). Men det går godt i mange anvendelser, hvor man ikke ser på de syge eksempler, matematikerne kan finde på 🙂

Og hvorfor skulle man dog gøre noget så indviklet? Jo, pointen er, at man i stedet for funktionen f(x) har koefficienterne – an’erne og bn’erne, som måler hhv. vægten af cos(nx) og af sin(nx) i f(x). I eksemplet tegnet ovenfor, er a3=1/2 og b1=1, mens alle andre koefficienter er 0. Man har repræsenteret sin funktion af tiden ved hjælp af frekvenserne, der indgår. Hvis signalet er pænt, vil næsten alle koefficienterne være 0 eller meget små, så man kan undvære dem, uden at lyden ændres.

Diskret Fourier transformation
Hvis man, som i mobiltelefonen har et signal repræsenteret ved en række tal, x0,x1,x2,…,xN (det kunne være højden af grafen for signalet til forskellige tidspunkter med f.eks 1/10 sekund imellem), kan man gøre noget lignende. Ligesom i den kontinuerte version, får man information om “svingning” – sin(7t) svinger hurtigere end sin(t), eller m.a.o. er periodisk med en kortere periode. Diskret Fourier transform afslører også periodicitet i data. Man kan så analysere signalet efter frekvenser – se hvor meget, det ligger i et givet frekvensområde. der er masser af matematik i dette område. Og smarte algoritmer .Eksempelvis Fast Fourier Transform, som udregner diskret fourier transformation (finder koefficienterne). Hvis nogen vil skrive noget om det til bloggen, så sig endelig til.

Jeg har lavet en Facebookgruppe, Numb3rs – dansk. Måske ses vi der 🙂

I tænketanken ville Alan lave strøm af kolort. Det kan man godt, siger f.eks Live Science. Matematik var der også: Billedbehandling, “voxel based 3D-capture”, invers spilteori og noget med varmesignaturer (thermo signatures).
Billedbehandligene hentydede til et tidligere program, Jack of All Trades, hvor Charlie genskabte et billede, der var forvansket, fordi det var en spejlig i et termokrus. Diffeomorphic matching, kaldte de det.
Kryptering
Amita omtalte 128bit kryptering – den kryptering, Charlie og co skulle bryde for at kunne standse bussen. der findes mange forskellige krypteringsmetoder, men her hentydes nok til blokvis kryptering. Man deler sin tekst op i stykker – her har de længde 128 bits (tænk bare på bogstaver). Man bruger så en krypteringsnøgle (som man skal holde hemmeligt – dette er ikke public key kryptering). Hver blok er krypteret for sig. Krypteringen indeholder flere skridt, som allesammen skal være effektive.
En substitution opererer på en del af blokke (de første fire bogstaver) og giver en lige så lang del ud igen. Man skal kunne dekryptere, så to forskellige blokke ind skal give to forskellige blokke ud (injektivitet elller 1-1).
Eksempel: 0101 ind, 1001 ud. I en god substitution, skal hvert bogstav i output afhænge af hvert bogstav i input, så man ikke kan bryde krypteringen ved at prøve med 0100 for at se, hvad sidste bogstav bliver til. Mellem substitutionerne sidder permutationsskridt, hvor alle 128 bits byttes rundt. På den måde bliver output fra substitutionerne blandet mellem hinanden og kan så puttes ind i nye substitutioner. Jeg har et skema fra Wikipedia:

Her er S substitution, P er permutation og K er “key”, nøgle. Man bruger altså nøglen flere steder – f.eks. kanman lægge nøglens værdier sammen med det ord, der er output fra den seneste substitution. (Det hele er binært – 0 og 1- og 0+0=0, 0+1=1, 1+1=0, så nå man adderer bliver de bits, hvor nøglen har værdi 0, bevaret, de andre bliver ændret – fra 0 til 1 eller 1 til 0).

Denne type kryptering er beregningsmæssigt effektiv bl.a. fordi den er oplagt at udføre parallelt – hver af S operationerne kan gøres samtidig, hvir man har flere processorer. Desuden er dekryptering nemt; Man løber bare nedefra og op.
Hver for sig er de enkelte skridt nemme at bryde. Substitutionskryptering og permutationskryptering er ikke stærk kryptering. Og at lægge nøglen til er heller ikke, hvis man bruger samme nøgle mere end en gang. Men alti i alt – med tilstrækkeligt mange kombinationer ef S og P, får man en stærk kryptering, hvor kompleksiteten af at bryde koden er eksponentielt afhængig af nøglens længde.
Eksempler på denne type koder er DES (Data Encryption Standard), IDEA (International Data Encryption Algorithm) og AES (Advanced Encryption Standard).
Man kan bryde krypteringen ved at finde nøglen – et brute force angreb. Men at prøve alle nøgler er langvarigt og energikrævende. 128 bits svarer til 2^128 ( 2 ganget med sig selv 128 gange)=
340,282,366,920,938,463,463,374,607,431,768,211,456.
Jeg har googlet mig til, at den energi, der mindst indgår i bare at løbe igennem alle disse nøgler er 10^18 Joule (og så regner man ikke – man skal jo prøve dem af og se, om de virker). Det svarer til 30 Gigawatt i et år. Man kan på Energinet se den aktuelle elproduktion i Danmark. Der produceres lige nu (15/4 klokken 09.03) inklusive import fra Sverige og Norge og fratrukket eksport til Tyskland 4705 MW. altså 4 Gigawatt.

Så skal man bryde krypteringen, skal man gøre noget smartere.

Voxelbased 3D capture
En voxel er en lille kasse. Hvor man på computerskærmen har en opdeling i (små) rektangler, opdeler man et område i rummet i voxels.
3D capture går ud på at finde det rigtige 3D objekt, som giver anledning til et antal 2D repræsentation – man ser det fra siden, oppe fra og nedefra. Dette er naturligvis et varmt emne; Man får data fra overvågning og skal udlede, hvad det rigtige objekt er (hvis man er i krigerisk humør, kan man tænke på diverse våben, men det kunne jo også være kattekillinger).

Vores hjerne er rigtig god til det – hvis ellers vi ser noget, vi plejer at se. Man forsøger at lave computerprogrammer, der kan genskabe menneskers positioner og bevægelser. Og helst hurtigt (i real time). En ikke-krigerisk anvendelse er handicaphjælpemidler, hvor det er smart, hvis robotter kan genkende objekter – og “forstå kropssprog”. Der er smuk geometri, smarte algoritmer og meget andet i dette område, men jeg stopper her – forskningen kalder. Se for eksempel hos German Cheung fra Carnegie Mellon. Eller hos Aalborg Universitets Computer Vision gruppe

Jeg har skrevet lidt på den danske Wikipedia-artikel om Numb3rs og tilføjet et link til bloggen. Og jeg har lagt et link ind på den engelske. Jeg ville også lægge et på den norske, men der var sandelig et allerede – vi har måske norkse læsere- herligt. Den danske side kan mildt sagt godt blive bedre, så der er en opgave for jer bloglæsere. Jeg har nok at gøre med bloggen.

Charlie filosoferede om entropi i starten – man hørte ham i baggrunden. Amita betegnede kommunikationen mellem Larry og Charlie som en test af grænserne for Shannons kildekodningssætning. Charlie brugte Viterbi algoritmer til at forudsige Buck Winters næste træk (noget med skjulte tilstande). Simpleksalgoritmen indgik i en optimering under randbetingelser : Hvor lang tid tager det at lave et godt reb af tandtråd givet mængden af tandtråd i fængslet – eller noget i den retning.

Entropi
Det har været på bloggen her før, og jeg tillader mig at gentage en del af det her; man skal jo ikke genopfinde det varme vand. Entropi kaldes populært for et mål for uorden, og det optræder både i fysik (i termodynamik) og i informationsteori.
Ideen om, hvordan man kan give et mål for mængden af information i f.eks. en besked, der skal sendes over nettet, skyldes Claude Shannon i artiklen A mathematical theory of Communication fra 1948, hvor han bl.a. definerer informationsmængden, entropien. Entropi defineres via sandsynlighedsteori; man skal have et mål for, hvor meget klogere, man er blevet af at få en bestemt information. Vi forudsætter, at man på forhånd har en ide om, hvad der sandsynligvis kunne ske. Er beskeden så, at noget, vi anså for meget usandsynligt, er sket, vil vi anse det for mere information, end hvis vi får vished om, at noget, vi allerede mente var ret sandsynligt, rent faktisk er sket. Er informationen udfaldet af at slå et slag med tre terninger, vil jeg blive mere overrasket over 3 seksere, end over 2 seksere og en treer, fordi det sidste er et mere sandsynligt udfald (der er tre måder, man kan få 2 seksere og en treer svarende til, hvilken terning, der giver en treer). Man vil også blive mere overrasket over at få at vide, at det regnede i San Francisco i juni, end at det regnede i København. Så man måler informationen udfra, hvad man ved om sandsynligheden for de forskellige mulige informationer.
Med formler:

H(X) er entropien af x1,…,xn, hvor sandsynligheden for xi er p(xi). b er grundtallet for den logaritmefunktion, der bruges. Ofte er b=2 – hvis informationen x1,…,xn er 0’er og 1’er. Mere præcist er x1,…,xn er de mulige  udfald af en stokastisk variabel X. Det modellerer kommunikation i den forstand, at man forestiller sig, visse bits (ord eller sætninger skulle det være, men her er det nok nærmere bogstaver) er mere sandsynlige end andre.

H(X) måler en middelværdi af informationsindholdet, I(x). Informationsindholdet i xi er log(1/p(xi)) =-log(p(xi). Informationsindholdet er altså stort, hvis sandsynligheden for xi er lille, – jo mere usandsynlig, xi er, jo mere information er der, når xi rent faktisk sker. Det opvejes så af, at der ganges med p(xi), når man udregner H. Hvis noget er meget usandsynligt, er der megen information i, men det sker jo så heller ikke ret tit.

Eksempel: Hvis alle udfald er lige sandsynlige, så er p(xi)=1/n. Altså er H(X)=log(n) =1, hvis vi bruger logaritmen med grundtal n. Hvis et udfald har sandsynlighed 1 og alle andre aldrig sker, så er H(X)=0. (Hvis p(xi)=0, er reglen, at p(xi)logp(xi)=0, selvom man ikke kan tage logaritmen til 0.). Andre værdier af H(X) ligger imellem 0 og 1 (når man bruger en passende logaritme.)

Et aspekt af informationsteori er at uddrage hvor lidt plads, der skal til for at repræsentere informationen – hvor mange bits eller bogstaver. De bits, der er overflødige er redundante. Hvis vi ved, beskeden handler om N gange plat og krone, hvor mønten er fair, altså sandsynligheden for plat er 1/2, så er vi nødt til at informere om alle udfald. Vi skal bruge NH(X) bits til at lagre informationen, hvor H(X)=1, altså strenglængde N. Shannons kildekodningssætning siger, at det gælder generelt: Hvis man slår N gange med en mønt, hvor plat har sandsynlighed p, altså H(X)=-( p log(p) +(1-p)log(1-p))=-(p log(p/(1-p))+log(1-p)), så kan man give informationen om udfaldet i en streng af længde NH(X) (eller længere naturligvis). -Der indgår en grænseovergang, så det gælder for lange strenge, og sandsynligheden for informationstab falder, jo længere streng, man vil lagre. Og omvendt: Bruger man kortere strenglængde, er man næsten sikker på at miste information.

Et andet aspekt af sagen er, at man faktisk ofte sender overflødig information med: Hvis man skal sende på en “kanal med støj”. Som f.eks. afspille en CD eller sende noget over nettet. Hvis beskeden risikerer at blive ændret lidt undervejs, vil man gerne kunne rekonstruere den. Det kan man f.eks., hvis man har sendt samme besked flere gange, altså sendt overflødig information. Men det kan gøres noget mere intelligent – det er det, kodningsteori beskæftiger sig med. Se f.eks. Olav Geils hjemmeside. Hvor meget ekstra information, der skal med, afhænger af, hvor meget støj, der er på linien. Men siger, at man indkoder – pakker informationen ind- inden afsendelse og dekoder, pakker den ud igen bagefter.

Shannons kanalkodningssætning siger, at uanset hvor støjfyldt en kanal er, så kan man finde måder at sende information over den uden tab af information, eller igen: med meget lille sandsynlighed for tab af information. Og sætningen siger, hvor god en kodning, man kan lave, i.e., hvor meget ekstra information er man nødt til at sende med, hvis der er en given mængde støj (sandsynlighed for fejl) og man kun vil acceptere en vis (lille) maksimal sandsynlighed for fejl i det budskab der når frem. Shannon giver ikke en opskrift på disse optimale kodningsalgoritmer – det er et forskningsområde at finde gode koder. Og at sørge for, at de ikke er for komplicerede i den forstand, at de skal have lav kompleksitet: Man skal ikke bruge rigtig lang tid på at indkode (skrive beskeden om, pakke den ind, inden afsendelse) og dekode (pakke den ud, når den kommer frem), for så kunne man måske lige så godt have sendt en længere streng i stedet for – have brugt en mindre effektiv kode.

Entropi er også et begreb i termodynamik – det får I ikke noget om nu, men måske senere. Det er igen et mål for “uorden”. Eksempelvis er en balje med lunkent vand mere uordentlig end en, hvor man havde koldt vand i og lige har hældt varmt i, som ikke har blandet sig med det kolde endnu. Og her er det klart: Entropien vokser – vandet blander sig og bliver lunkent. Og det er karakteristisk, at man ikke kan gå tilbage og skille hurtige molekyler (varmt vand) fra langsomme. Det er det, de mener med “arrow of time” – det går kun en vej, og det fortæller hvad tidsretningen er.

I Frienemies fortæller Charlie om denne gåde, som Martin Gardner oprindeligt har stillet. Gardner er kendt for logiske gåder i bl.a. Scientific American og en stribe bøger.
I en truel er der tre personer a,b,c. De er ikke lige gode til at ramme. A dårligst (rammer i Charlies version 1/3 af gangene), B rammer 2/3 og C rammer altid. De skyder efter tur, A først. Nu er pointen, at A er mest interesseret i, at de to andre skyder efter hinanden, da de er bedre til at tage livet af hinanden, end A vil være. Så A skyder med vilje ved siden af (ifølge Gardner- Charlie siger, A skyder efter B, men det giver ikke helt mening, for hvis han rammer, vil C med garanti skyde A.) Nu skyder B efter C, da det er den største trussel. Så skyder C og rammer B.
Dette afhænger jo af, hvad målet og reglerne er: Hvor mange skud har de? Skal de blive ved til to er døde? Kan man såre og ikke dræbe? Etc.
Skal de ikke blive ved til døden kunne både B og C vel vælge at skyde ved siden af, og alle går derfra med livet i behod. Man skal altså have mere specifikke regler og mål, før man kan se en strategi, hvis der er en.