Numb3rs

Jeg skrev tidligere en meget kort notits om, at Abelprisen i år går til John W.Milnor.
På Abelprisens website kan man læse beskrivelser af, hvad Milnor fik prisen for – både på norsk og engelsk.

John W. Milnor, som man ser på billedet, er en af mine matematiske helte. Han har bidraget til flere områder af matematikken, han skriver fantastisk gode artikler i den forstand, at han virkelig gør sig umage for at forklare sig. Derfor er hans bøger også meget brugte. Både som kursusmateriale og som referencer for matematikere, der gerne vil lære noget nyt.
Milnors første artikel er publiceret, da han var 19 år gammel. Imponerende. Og den er publiceret i det meget ansete tidsskrift Annals of Mathematics.
Milnors efte min mening mest overraskende resultat er fra 1958. Det handler om, at der findes “eksotiske” kugleflader. Af dimension 7.
Jeg snyder og snupper forklaringen fra Timothy Gowers’ beskrivelse af Milnors arbejde.

“First, let me express in a different way what it means for exotic spheres to exist. It means that you can take a sphere and continuously deform it to form another shape that is also smooth, in the sense of not having any “corners”; however, even though the original sphere is smooth and the continuously deformed sphere is smooth, the only deformations that turn one into the other are not smooth.”

Milnor viste, at der er 27 eksotiske kugleflader af dimension 7 (foruden den sædvanlige kugleflade af dimension 7, som er de punkter (x1,x2,…,x8), som opfylder x1^2+x2^2+…+x8^2=1.)
Det var et væsentligt resultat, fordi matematikerne indtil da var overbeviste om, at alle kontinuerte deformationer kunne “glattes ud”. Lidt som når man stryger en skjorte. Man kan sige, problemet er, at noget høj-dimensionalt kan krølle på en meget kompliceret måde, så man flytter folden med rundt og ikke kan komme af med den. Det var starten på en lang matematisk udvikling: Når nu intuitionen havde været forkert, hvad kunne der så ellers gemme sig af mystiske fænomener. Jeg kan godt læse og forstå artiklen, (den er selvfølgelig velskrevet) men resultatet er alligevel meget mærkeligt.

Milnor har bidraget til mange andre områder af matematikken, f.eks. kompleks dynamik – det, man ser bileder af, når man ser Mandelbrotmængden og lignende farverige illustrationer. I kan læse mere på linket ovenfor.
I øvrigt er Milnors seneste artikel fra 2010. Og han fyldte 80 i februar i år. Lifetime achievement, kan man roligt sige.

Jeg er nødt til at begynde med at brokke mig: Hvad i alverden går der gennem hovedet på Numb3rs-forfatterne, når de lader Amita, ass.prof i matematik ved et topuniversitet, bruge sin tid på at skaffe jakkesæt til David. Det er da helt ude i hampen. Hvadenten hun har god smag eller ej.
Nå, men matematikken. Jeg så noget risk/reward analyse. Charlie fortalte om, hvordan dyr laver den slags analyser, når de søger føde. Det var det, de viste, med musene, der skulle finde føde på en mark, hvor de samtidig blev jaget af en musvåge.
Der var noget om beregning af sandsynligt landingssted for faldskærmsudspringeren, forudsat kendskab til vind og vejr og terræn.

Risk/reward
Det er et kæmpe område, som (naturligvis) er vigtigt i finansiering, men som også studeres i biologi, sådan som Charlie beskrev det. jeg har fundet en fin reference: Optimal Foraging Theory: Constraints and Cognitive Processes. Det er kapitel 6 i en biologibog. Der er lavet mange eksperimenter med dyr, hvor man undersøger, om de er risikovillige eller ej. Det afhænger, så vidt man kan se, af, om de er sultne eller ej. Og om de har unger, de skal fodre på. Forsøgene her var med fugle og (humle) bier, og risikoen var, om der var store mængder mad med en vis sandsynlighed (og ingenting med en vis sandsynlighed), eller mindre mængder med sikkerhed. (Statistikerne ville sige, at der er samme middelværdi men forskellig varians.) Man skal tage hensyn til, at dyrene måske ikke husker langt tilbage, så de har måske ikke fornemmelse af gennemsnittet, men kun det, de fik sidste gang. I andre forsøg har man givet rotter mad med eller uden risiko for elektrisk stød. De løber gerne risikoen, hvis der er nok mad.
Charlie siger, at han kan se, at forbryderne må have været desperate. Altså: For at løbe så stor en risiko, skal man virkelig være “sulten”, hvis man er en rotte.

En analyse af risiko kontra udbytte for et dyr kunne være målt i energi: Hvor meget energi skal bruges på at få fat på bytte, som giver en vis energi. For stære, der fodrer nger, optimerer de den energi, ungerne får – de brger energi på at vente, forældrene bruger energi på at flyve. Derfor flyver forældrene tidligegt tilbage – de kunne have plads til mange larver i næbbet (og de bruger ikke megen energi på at samle flere), men ungerne bruger energi mens de venter.

For bier bliver det mere og mere besværligt/energikrævende at flyve, jo mere nektar, de allerede har samlet. Så hvad er optimalt for en bikube? Skal den enkelte arbejderbi skaffe mest muligt på kortest tid (og falde død om for tidligt), eller skal den flyve hjem ind imellem for ikke at blive overbelastet? Det ser ud til, bikuber sætter værdi i deres arbejdsbier. I hvert fald passer modellen med, at de flyver hjem ind imellem, bedst til data. Det er der en fin graf over i referencen ovenfor, men jeg kan ikke kopiere den herover, så I må selv kigge efter…
For bier, der testes for risikovillighed, opstår en ny problematik: Hvor mange besøg ved en blomst kan de huske? I kapitlet ovenfor forestiller man sig, at bier kan regne gennemsnit ud af to besøg ved en gul blomst. Og sammenligne med besøg ved en lilla. Hvis den gule nu giver 6 enheder pollen med sandsynlighed 1/3, og den gule giver ingenting med sandsynlighed 2/3. Den lilla giver 2 enheder hver gang. Hvad kan humlebien så regne ud?
Den besøger to gule blomster, lagrer informationen om gennemsnitligt udbytte og får
I gennemsnit (6+0)/2=3 med sandsynlighed 2×1/3 x2/3= 4/9
I gennemsnit (6+6)/2=6 med sandsynlighed 1/3 x1/3 =1/9
I gennemsnit 0+0/2=0 med sandsynlighed 2/3×2/3=4/9
Den sammenligner med den lilla blomst, og vil så mere end halvdelen af gangene ende med at foretrække den gule. Men det gennemsnitlige udbytte er naturligvis 2 enheder. 3x 4/9 + 6x 1/9 =18/9=2
Biologerne har regnet på forskellige mulige strategier – bien kunne skifte til en anden farve blomst, hvis den ikke finder noget (men så vil den jo efter kort tid holde sig til de lilla). Det er, som vi har set før, opstilling af en model, som man sammenligner med data.
Andre modeller forudsætter, at der er noget tilfældighed involveret. Men, som garvede Numb3rs læsere vil vide, så skal man overveje, hvilken struktur der er i tilfældighederne. På
Optimal Patch Exploitation fra Wolfram Demonstrations Project er en animation af daphnier, der udforsker et område ved at bevæge sig i ryk, dreje en vinkel, så et nyt “hop”. Vinklerne vælges med en vis sandsynlighedsfordeling. Nu kan man så se, hvad virkelige daphnier gør, om det er optimalt, om det passer til en af modellens muligheder, om der er andre muligheder, der ville have været bedre.

Drop Zone
Der er faktisk formler for, hvor faldskærmsudspringere ender henne.
Jeg har Googlet mig til lange instruktioner for amerikansk militær. En formel er D=KAV formlen D er afstand til ønsket landingssted. K er en konstant, som er 3, hvis det er frit fald og 25, hvis det er en faldskærm (her smider de nu nok udstyr ud, må man håbe). A er flyvehøjden målt i 1000 fod. V er den gennemsnitlige vindhastighed målt i knob. Vinden er beregnet med en retning – så der er en vinkel i grader involveret (smart nok tænkt…)
Man bruger den også omvendt til at finde HARP, High Altitude Release Point udfra de andre data. Konstanten K afhænger i øvrigt af typen af faldskærm – hvor godt den svæver.

Denne gang fik Charlie faktisk brugt noget matematik: Kombinatorisk spilteori, en variation over Dijkstras korteste vej algoritme, noget om en laserlæser (mystisk ord på dansk…), som opfangede signaler fra tasterne på et computertastatur. Og så skulle Charlie og Amita have holdt forelæsning om den multivariate hypergeometriske fordeling.

Kombinatorisk spilteori
Spilteori har vi set på flere gange på bloggen – I kan bruge søgefeltet, hvis I vil se mere. Denne gang var det kombinatorisk spilteori. Det drejer sig om to-personers spil, der er perfekt information: Begge spillere kan se, hvad den anden gør, og kender konsekvenserne af egne handlinger. (I modsætning til fangernes dilemma, hvor pointen er, at man ikke ved, hvad den anden gør – eller med en anden formulering: Begge skal bestemme sig samtidig, om de vil tilstå eller holde mund).
Man skiftes til at “trække”.
Mange sædvanlige spil er hører under denne overordnede ramme: Skak, dam, kryds og bolle, Go, Mølle,… Men ikke kortspil, hvor man sædvanligvis ikke har fuld information.

Taber er enten den, der ikke kan flytte mere. Eller den, der flytter det sidste mulige flyt.

Eksempel: Hex er et spil for to som ovenfor, og det er en rigtig god historie, så den får I. Det blev opfundet af Piet Hein i 1942, og det indeholder mange interessante matematisk-datalogiske problemstillinger. Piet Hein sagde selv, at han fik ideen, da han overvejede 4-farveproblemet. Thomas Maarup, matematikstuderende i Odense, skrev speciale om Hex og dets historie i 2005. Det skrev Information en artikel om. Piet Hein skrev en del om spillet i Politiken, hvor det gik under navnet Polygon, mens han selv kaldte det Con-Tac-Tix. Politikens artikler involverede læserne i at finde gode strategier, gode modoffensiver til givne strategier etc. og man kan se reklamer for spillet, herunder en, der forestiller nogle Hex-spillere i beskyttelsesrum (det var jo under 2.Verdenskrig), som ikke vil komme op, før de har spillet færdig.
I 1949 blev det genopfundet af John Nash (ham, der er portrætteret i filmen “A beautiful Mind”. Han fik Nobelprisen for spilteori.) De studerende på Princeton University kaldte det Nash eller John (en myte er, at det hed John, fordi de spillede det på mosaikkerne på badeværelsesgulvet, og John er slang for toilet… Men det er nu en myte ifølge bogen A beautiful Mind.) Spillet blev lavet kommercielt af et amerikansk firma, som døbte det Hex.

I Hex har man et bræt inddelt i sekskantede (hexagonale) felter. To spillere sætter hhv. sorte og hvide brikker (eller røde og blå). Målet er for begge at danne en sammenhængende sti på tværs af brættet (og forhindre den anden i det). På billedet kan man se, at stierne løber “på tværs” af hinanden.

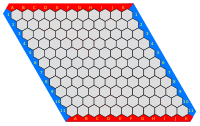
Hex er et godt spil, idet det ikke kan ende uafgjort: Hvis en spiller er forhindret i at lave en sammenhængende sti på tværs, er det fordi den anden har lavet en.
Vindende strategi
En strategi er en opskrift, som en af spillerne kan bruge til i hvert eneste træk at analysere det, der hidtil er sket, til at sætte en ny brik.
Strategien er vindende, hvis …. jeps, hvis den spiller, der bruger strategien, altid vinder.

Et spil, der
1) altid slutter efter endeligt mange træk med en vinder
2) Har perfekt information
er “determined”, i.e., der er en vindende strategi for en af spillerne. Argument:
Spiller I spiller for ikke at tabe: I hvert træk spiller I for at sikre, at spiller II ikke har en vindende strategi efter spiller I’s træk. Hvis ikke Spiller I kan gøre det, må spiller II have en vindende strategi. Omvendt, hvis spiller I kan det, vil spiller II ikke vinde, og det vil spiller I altså, eftersom spillet er slut efter et endeligt antal træk. Så det var en vindende strategi…

Der er altid en vindende strategi i Hex for den, der begynder spillet, men man ved ikke, hvad den er – kun, at den eksisterer. Beviset er et såkaldt strategirøveri. Først viser man, at en af spillerne har en vindende strategi (det har vi gjort); og derefter, at hvis det er for spiller nummer 2, kan første spiller stjæle strategien ved at lade somom, den første brik bare blev sat tilfældigt. Det virker, fordi det ikke kan være en ulempe at sætte en ekstra brik.

Man kan nu undre sig over, at man ikke bare kan regne alle tilfælde igennem og bestemme en vindende strategi. Det kan man for små spil (med lille bræt). Men dettager rigtig lang tid, og bruger rigtig meget plads på en computer at lave sådan en analyse.

Man forestiller sig en algoritme, der kan svare ja eller nej til, om en placering af en brik er et led i en vindende strategi. Pladsen, der skal bruges til analysen, vokser med sidelængden, n, af brættet. For et 10×10 bræt, er der 10^39 mulige positioner for brikkerne. Så det fylder meget. Faktisk er spørgsmålet om Hex PSPACE fuldstændigt – den plads, en algoritme som beskrevet her, kræver, vokser som et polynomium i n. Og alle andre PSPACE problemer kan oversættes til Hex, så en algoritme for Hex giver en for alle de andre. PSPACE problemer er, tror man i hvert fald, værre end NP problemer. NP-problemer er problemer, hvor man kan ” finde en løsning” til et ja/nej spørgsmål. PSPACE handler om at checke, om en løsning virker fremover, uanset, hvad den anden spiller gør. Og det ser jo umiddelbart værre ud. Men man ved det ikke.

Læs mere om matematikken f.eks. på Mathworld

Eller du kan jo også bare spille det – eksempelvis online på boardspace.net. Der findes også apps, så man kan spille på sin smartphone – se f.eks. de eksterne links under Wikipedia.

Lige nu bliver det annonceret på http://www.abelprisen.no/no/, at John Milnor, Stony Brook får Abelprisen 2011

Ian Edgerton mente Charlie kunne hjælpe ham, og det kunne han minsandten.
Matematikken var Pursuit-Evasion, som vi har haft tidligere på bloggen, der var spilteori, Charlie nævnte syntetisk differentialgeometri som en analogi til noget svært, tror jeg nok, der var “Longitudinal socialization process” og en del om mønstre og netværk.

Pursuit Evasion
Det kan dække over flere ting. Jeg har skrevet om det i afsnittene To døtre, Spree og Mørkt Stof

En version af Pursuit Evasion drejer sig om en forfølger og et bytte. Forfølgeren kan se byttet, og løber hele tiden hen mod byttet. Hvordan det ender, omme an på, hovr hurtigt, de begge løber, og hvilken kurve, byttet løber på.
Hvis byttet løber på en linje, er forfølgerens kurve en tractrice, eller hundekurve:

Her er forskellige eksempler, hvor byttet løber på en cirkel med konstant fart:

Illustrationerne er fra Mathworld. I kan læse om ligningerne bag – differentialligninger – på “Spree” linket, men jeg kopierer det ind her som en service 🙂
Vi beskriver en kurve i planen ved en parameterfremstilling: (x(t),y(t)), hvor t er tiden. Man kan altså løbe på en linie ved f.eks.
x(t)=t
y(t)=2t+3
Så er man i punktet (2,7) til tiden t=2, og man er i (0,3) når t=0, og man løber med konstant fart. Man kan løbe på den samme linie med f.eks.
x(t)=t^3
y(t)=2t^3+3

hvor t^3 betyder t i tredie.
Her er man stadig i (0,3) når t=0, men man er i (8,19), når t=2. Man løber ikke med konstant fart.
Kald nu forfølgerens kurve
F(t)=( f1(t), f2(t))
og undvigerens
U(t)=(u1(t),u2(t))

Betingelsen om “ren” forfølgelse – pure pursut – siger, at vektoren
U(t)-F(t)=(u1(t)-f1(t),u2(t)-f2(t))

er parallel med forfølgerens hastighedsvektor – forfølgeren løber direkte mod byttet.
F’(t)=(f1′(t),f2′(t))

og man får således en differentialligning, som beskriver forfølgerens hastighedsvektor udfra forfølgerens position og undvigerens position. Hvis forfølgeren løber med konstant fart k, bliver ligningen

F’(t)=k(U(t)-F(t))/|U(t)-F(t)|

eller rettere

f1′(t)=k(u1(t)-f1(t))/|U(t)-F(t)|
f2′(t)=k(u2(t)-f2(t))/|U(t)-F(t)|

hvor |U(t)-F(t)| er længden af vektoren. Hvis vi nu kender U(t) – altså forfølgerens kurve – kan vi opstille ligningen. Vi har også resultater, der siger, at den slags ligninger har løsninger (under passende forudsætninger om U(t)), men generelt kan vi ikke skrive en løsning op med pæne formler.

Til gengæld kan vi få en computer til at regne en løsning ud stepvis: Man lader forfølgeren gå et lille stykke langs linien, der peger mod undvigeren. I mellemtiden har undvigeren flyttet sig, så man får en ny linie, man løber et lillebitte stykke ad. Og så fremdeles. Man laver altså en kurve af små bitte stykke linie. Det kan gøres lidt mere intelligent, end beskrevet her, og man kan få en løsningskurve, der er så tæt på den rigtige, som man vil have det.

En anden version af pursuit evasion bruges, når man vil have robotter til at afsøge et terræn. Robotterne har et vist synsfelt, de skal holde øje med et område, og ingen må undslippe. At beregne, hvor mange robotter, der minimum skal bruges til et givet område, er NP-hårdt. Det kan man læse mere om her på Stanford. Her er deres algoritme i brug på et ganske indviklet område. Der er en robot. Det gule er det, den kan se. Det hvide er sikkert, og det går kan stadig gemme “fjender

Find matematik i din by, og fortæl om det til Maths in the city projektet.
Der er fine eksempler på hjemmesiden. Konkurrencen løber fra 4.april til 3.maj.
Da Christopher Wren skulle bygge Sheldonian Theater i Oxford fandt han på at lade bjælker understøtte hinanden, som man ser eksemplificeret her

Han måtte løse 25 ligninger med 25 ubekendte for at vise, at hans system var stærkt nok til at bære loftet. Jeg ved ikke, om de var lineære. Det var de nu nok ikke, hvis det er noget med kræfter. Men det er under alle omstændigheder besværligt at gøre i hånden.

Her var fokus på forskellen på det virtuelle og virkeligheden. En hacker havde ikke overvejet, at handlinger på nettet har konsekvenser. Ovenikøbet var det, der foregik, tyveri af identitet i form af CPR, bankkontonummer etc. Ganske skræmmende, og et incitament til at holde egne data og passwords tæt til kroppen, hvad så end det betyder på nettet…
Jeg så en del matematikrelaterede emner: Leet – nørdsprog, som jeg, der ellers er lykkelig i nørdland, ikke kendte. Kryptering, Diverse om Internettet: DNS, IRC og måder, man kan snyde det på.
Og så var der en 3d-printer. Sådan en ønsker jeg mig. Jeg synes, det er rigtig smart og fascinerende, at man nu kan få lavet 3d figurer til en forholdsvis rimelig pris.

Leet
Når Numb3rs har et 3-tal i stedet for e, er det en slags leet. Leet eller elite, er et “skriftsprog”, som betår i at indsætte tegn i stedet for bogstaver. Der er mere i det end det – og “dialekter”, så det er ikke bare en substitution. Leet kan f.eks. skrives l33t eller 1337 eller £33+ eller … Der er Leet-versioner af Google – her på dansk. Det stammer fra gamle dage – da jeg var ung- og man brugte Bulletin Boards – leet er en smart måde til at omgås filtre på, og man kan holde de nye (n00bs for newbies) udenfor ved at skrive noget, kun de indviede forstå. Det betyder jo også elite…
På f.eks. denne side kan man indtaste tekst og få den oversat til (en version af) leet.

3d-printere
Der er forskellige teknologier til 3d-print, fælles er, at man opdeler sit 3d-object i “skiver”, som så printes en skive ad gangen. Og så klistres det enten undervejs eller til sidst.
At opdele rumlige objekter i skiver er velkendt i matematik. Archimedes regnede rumfang ud af rumlige objekter på den måde – opdeling i smallere og smallere skiver… integration.

Et ret morsomt projekt er CandyFab, et projekt fra Evil Mad Scientist, hvor de printer 3d sukkerfigurer.

Her er et Möbiusbånd fra Evil Mad Scientist.
Som man nok kan se, er det ikke simpelt at opdele et 3d-objekt i skiver. Det kræver en eller anden matematisk model – Har man beskrevet objektet med en ligning i 3 variable, er det i princippet let nok:
En kugle har ligning x^2+y^2+z^2= R^2, hvor R er radius. Hvert lag svarer til et inteval i z-koordinaten e.g. 0< =z<=0,1 (vi skærer i skiver langs z-aksen). Og vi får, ikke overraskende cirkler x^2+y^2=R^2 – s^2 hvor s er et tal i intervallet, hvor vi skærer. Hvis skiverne er smalle nok, kan man ikke se, figuren bliver lidt kantet.
En anden mulighed er at “kopiere” et 3d objekt ved at scanne det – det giver en matematisk repræsentation af punkter på overfladen af objektet – og så printe.

RepRap from Adrian Bowyer on Vimeo.

RepRap er en 3d printer, der kan printe sig selv … så man kan printe en ny printer til vennerne.

Her fortæller Anthony Atala fra Wake Forest Institute for regenerative medicine om 3d-print af organer – ved brug af stamceller. Det er fra TED talks, hvor man kan finde både godt og skidt.

Indtil man får sin egen 3d printer – til sukker eller plastic- kan man prøve en DTU’s Mathematicum (nej nej, jeg er ikke misundelig 🙂 ). Vi har også 3d-printere i Aalborg, men jeg har ikke en, jeg må lege med 🙁

På Poul Høis blog på b.dk foreslås, at alle forskere bør blogge. Her har jeres blogmoster naturligvis i proncippet ren samvittighed. Men ideen skulle være, at vi skal skrive om egen forskning. Jeg synes ikke, det giver mening for matematikere. Vi skal kunne forske i noget, der er svært nok til, at vi ikke kan forklare det til alle. Selvfølgelig kan vi forklare noget om overordnede mål for vores område, men de konkrete artikler skal man altså ikke kunne forklare. Nogen må forklare Poul Høi, at det giver dårlig valuta for forskningspengene, hvis vi kun må forske i det, vi kan forklare til alle. Det er et målepunkt af typen Fra forskning til faktura, og det er ikke smart.
Jeg forsker jo. Og bruger min indsigt i matematik til at skrive blog om mangt og meget med udgangspunkt i Numb3rs. Herunder ofte fra forskningsfronten. Men ikke nødvendigvis min egen forskning. Det ved I jo godt, hvis I plejer at kommer her på bloggen. Jeg skriver faktisk bl.a. dette, fordi Sidsel Jensen har været så venlig at linke her til Numb3rs i kommentarsporet til Høis blog. Så måske kommer nogen forbi via det link.
I skal være meget velkomne!

Jeg spottede en del fysik, og dermed jo også matematik – fysikere beskriver Verden ved brug af matematik. Der var en “Laser Induced plasma channel”, en LIPC. Det er den, der laver lyn, og som er for kraftig, så den slår folk ihjel. En lille smule Googling viser, at der har været forsøg med den slags, men det ser ikke ud til at være lykkedes. Hvilket det jo heller ikke gør i Numb3rs. Det er en slags Taser, som ikke skal sende elektroder ud. Men som sagt er det ikke lykkedes at få det til at virke (tror jeg da).

Her er en YouTube video med en mini LIPC. Hvis altså ikke det er et falsum.
Lyn og fysikken bag, kan man læse om hos dmi. Der er stadig fænomener om lyn, fysikerne ikke kan forklare – eksempelvis, hvordan der opbygges en spændingsforskel inde i en tordensky. Det er formentlig noget med iskrystaller, sådan som Charlie forklarede det, men så vidt jeg kan læse mig til, er fysikerne ikke enige om det. Det er jo opmuntrende for potentielle fysikere: Der er noget at gå igang med
Den mystiske Pentagonmedarbejder hentyder til Amitas arbejde med Satellit Telemetri.
Her kan man læse om lyn og lynafledning. Det er der matematik i, så det er det, I får denne gang. Det er jo også væsentligt, hvis man vil bygge en LIPC, at man kan styre, hvor meget man rammer. Men jeg må indrømme, det var lidt småt med matematikken i dette Numb3rsafsnit. Vi må håbe, det bliver bedre på onsdag…
Lyn
De fleste lyn har en strømstyrke på 20000-40000 Ampere. Men der forekommer større strømstyrker, og skal man lave lynafledning regner man derfor med såkaldte 98% parametre, hvor man sikrer sig mod 98% af de lyn, der kommer. Der regnes med 200000 Ampere, Specifik energi 10MJ/Ohm og ladning 200As. Strømstigningen er 200000 A/mikrosekund (Man regner på, hvor hurtigt strømstyrken går fra 0 til de 200000A. Det tager altså 1 mikrosekund.) Dette er beskyttelse på niveau I.
Bekyttelse i kategori II er beskyttelse mod 95% af alle lyn. Og så kan man nøjes med 150000 A. For 90% skal man kunne klare 100000A.
Fra Ohms lov ved vi, at spændingsfaldet er produktet af modstand og strømsstyrke (U=RI), så ved en modstand på 1 Ohm, er der et spændingsfald på 200000 V.
Modstanden fra hoved til fod i et menneske er 400-1200 Ohm, ifølge f.eks. artiklen “Lightning hazards and risks to humans: some case studies” M. Szczerbinsky. Journal of Electrostatics, 2003.
Livsfarligt er 30J, så den specifikke energi for et livsfarligt lyn er, hvis vi regner modstanden i en person til 800 Ohm, 30J/800 Ohm= 0,0375 J/Ohm. Lyn er altså farlige. Men det ved vi jo godt.

Pointen er, at hvis lynet rammer et materiale, der leder godt (har lille modstand), vil det ledes videre gennem metallet via de frie elektroner, ligesom sædvanlig strøm. Og det er det, en lynafleder gør.

Der er statistik i lyn: Hvor sandsynligt er det, at man rammes af lyn, og at en bygning rammes af lyn? I Danmark er der en gennemsnitlig lyntæthed på 0,23 lynnedslag pr kvadratkilometer pr år. Men der er både geografiske variationer og sæsonvariationer.
85% af lynnedslagene sker i juni, juli og august. 5% i maj, 5% i september og de sidste 5 % i perioden oktober til april (inklusive). (Kilde: DMI – se link ovenfor).
Geografisk er der flest lynnedslag i den sydvestlige del af landet.
MEN: Det skal tages med et gran salt:Statistikken bygge på lynregistreringer i perioden 1991-2000, og der var et kraftigt tordenvejr i juni 1994 i Nyborgområdet, som fylder meget i statistikken. (2000 lynnedslag pr 1000 kvadratkilometer i det område i 1994)
Vindmøller er jo høje strukturer. En vindmølle vil i gennemsnit blive ramt af
(gennemsniligt antal lyn pr kvadratkilometer på det sted, hvor møllen står)x(Vindmøllens effektive areal).
Det første tal får man fra lynstatistikken. Det andet er en funktion af vindmøllens højde. For en 150 m høj, tynd konstruktion, som en mølle, er det 0,7; er den 100m, er det 0,3 begge tal er kvadratkilometer. Tallene har jeg
fra rapporten Rekommandation 25 fra Dansk Energi.

Lynnedslag i en radius på r km kan “inducere skadelige overspændinger”. Det gennemsnitlige antal nedslag indenfor den afstand er (naturligvis)
(gennemsnitligt antal lyn pr kvadratkilometer)x pi x r^2
Værdien af r afhænger af jordens ledningsevne omkring møllen.
Desuden kan nedslag i elledninger, der leder hen til møllen, have skadelig virkning, hvis de slår ned tæt nok på møllen. Hvor tæt, det er, afhænger af ledningstypen.

Personer, der befinder sig i nærheden af møllen kan komme til skade, hvis lynet slår ned i møllen, eller i terrænet omkring den. Man skal beskytte møllen, så risikoen for personskade er højst 10^(-5). Altså risiko 1:100000 pr år for personskade.

Man skal sætte lynafledere, så et lyn møder aflederen, før bygningen. Til det bruges “rolling spheres” metoden: Et lyn, der er på vej gennem luften 20 m. fra møllen, kan slå ind på møllen.
Hvis et lyn er nået til punktet p, og møllen er indenfor kuglen med centrum i p og radius 20 m, kan det altså slå ind. Man “ruller kugler” med radius 20m rundt om møllen. Der, hvor de rører, skal møllen være forberedt til lynnedslag. Det er næsten hele møllen.

Bygninger med andre geometrier har ikke berøring med de rullende kugler i nær så mange punkter.

Numb3rs er tilbage efter jule- og vinterferien. Onsdag 2/3 klokken 20.00 vises afsnit nummer 108. Eller 6-06. Afsnittet hedder Drømmeland (Dreamland), og der er noget om UFO’er, har jeg læst.
Mere om dette senere.